Online Calculator: Simplex Method

The number of constraints:

------

The Number of variables:

------

Enter the values of the objective function:
F(x) = x_₁ + objective function inputselect of objective function	x_₂ + objective function inputselect of objective function	x_₃ + objective function inputselect of objective function	x_₄ → objective function inputselect of objective function

Enter the values of the system of constraints:
x_₁ + system of constraints input	x_₂ + system of constraints input	x_₃ + system of constraints input	x_₄ system of constraints input	select system of constraints system of constraints input
x_₁ + system of constraints input	x_₂ + system of constraints input	x_₃ + system of constraints input	x_₄ system of constraints input	select system of constraints system of constraints input
x_₁ + system of constraints input	x_₂ + system of constraints input	x_₃ + system of constraints input	x_₄ system of constraints input	select system of constraints system of constraints input
x_₁ + system of constraints input	x_₂ + system of constraints input	x_₃ + system of constraints input	x_₄ system of constraints input	select system of constraints system of constraints input

Solution example

F(x) = 3x₁ + 4x₂ → max

000	2x₁ + x₂ ≤ 600
	0x₁ + 0x₂ ≤ 225
	5x₁ +4x₂ ≤ 1000
	2x₂ ≥ 150
	0x₁ + 0x₂ ≥ 0

F(x) = 3x₁ + 4x₂ + 0x₃ + 0x₄ + 0x₅ + 0x₆ + 0x₇ - Mx₈ - Mx₉ → max

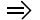
000	2x₁ + x₂ + x₃ = 600
	+ x₄ = 225
	5x₁ + 4x₂ + x₅ = 1000
	2x₂ - x₆ + x₈ = 150
	- x₇ + x₉ = 0

Preliminary stage: arrow down description

The preliminary stage begins with the need to get rid of negative values (if any) in the right part of the restrictions. For what the corresponding restrictions are multiplied by -1. After this manipulation, the sign of inequality is reversed.

Next, you need to get rid of inequalities, for which we introduce compensating variables in the left-hand side of the inequalities. If an inequality of the form ≤, then the compensating variable has the sign +, if the inequality of the form ≥, then the compensating variable has the sign -. Compensating variables are included in the objective function of the problem with a zero coefficient.

Now in the constraint system it is necessary to find a sufficient number of basis variables. Each constraint must have one basis variable. The basic is a variable that has a coefficient of 1 with it and is found only in one constraint. If there are no basis variables in some restriction, then we add them artificially, and artificial variables enter the objective function with the coefficient -M if the objective function tends to max and M, if the objective function tends to min.

Iteration: 1

B	Cb	P	x₁	x₂↓	x₃	x₄	x₅	x₆	x₇	x₈	x₉	Q
B	Cb	P	3	4	0	0	0	0	0	-M	-M	Q
x₃	0	600	2	1	1	0	0	0	0	0	0	600
x₄	0	225	0	0	0	1	0	0	0	0	0	∞
x₅	0	1000	5	4	0	0	1	0	0	0	0	250
x₈ ←	-M	150	0	2	0	0	0	-1	0	1	0	75
x₉	-M	0	0	0	0	0	0	0	-1	0	1	∞
max		-150M	-3	-2M-4	0	0	0	M	M	0	0

Calculation of table elements: arrow down description

Elements of the column basis (B)

Transfer to the table the basic elements that we identified in the preliminary stage:

B₁ = x₃;

B₂ = x₄;

B₃ = x₅;

B₄ = x₈;

B₅ = x₉;

Cb column items

Each cell of this column is equal to the coefficient, which corresponds to the base variable in the corresponding row.

Cb₁ = 0;

Cb₂ = 0;

Cb₃ = 0;

Cb₄ = -M;

Cb₅ = -M;

Values of variable variables and column P

At this stage, no calculations are needed, just transfer the values from the preliminary stage to the corresponding table cells:

P₁ = 600;

P₂ = 225;

P₃ = 1000;

P₄ = 150;

P₅ = 0;

x_1,1 = 2;

x_1,2 = 1;

x_1,3 = 1;

x_1,4 = 0;

x_1,5 = 0;

x_1,6 = 0;

x_1,7 = 0;

x_1,8 = 0;

x_1,9 = 0;

x_2,1 = 0;

x_2,2 = 0;

x_2,3 = 0;

x_2,4 = 1;

x_2,5 = 0;

x_2,6 = 0;

x_2,7 = 0;

x_2,8 = 0;

x_2,9 = 0;

x_3,1 = 5;

x_3,2 = 4;

x_3,3 = 0;

x_3,4 = 0;

x_3,5 = 1;

x_3,6 = 0;

x_3,7 = 0;

x_3,8 = 0;

x_3,9 = 0;

x_4,1 = 0;

x_4,2 = 2;

x_4,3 = 0;

x_4,4 = 0;

x_4,5 = 0;

x_4,6 = -1;

x_4,7 = 0;

x_4,8 = 1;

x_4,9 = 0;

x_5,1 = 0;

x_5,2 = 0;

x_5,3 = 0;

x_5,4 = 0;

x_5,5 = 0;

x_5,6 = 0;

x_5,7 = -1;

x_5,8 = 0;

x_5,9 = 1;

Objective function value

We calculate the value of the objective function by elementwise multiplying the column Cb by the column P, adding the results of the products.

Max_P = (Cb₁ * P₁) + (Cb₁₁ * P₂ + (Cb₂₁ * P₃ + (Cb₃₁ * P₄ + (Cb₄₁ * P₅ = (0 * 600) + (0 * 225) + (0 * 1000) + (-M * 150) + (-M * 0) = -150M;

Evaluated Control Variables

We calculate the estimates for each controlled variable, by element-wise multiplying the value from the variable column, by the value from the Cb column, summing up the results of the products, and subtracting the coefficient of the objective function from their sum, with this variable.

Max_x₁ = ((Cb₁ * x_1,1) + (Cb₂ * x_2,1) + (Cb₃ * x_3,1) + (Cb₄ * x_4,1) + (Cb₅ * x_5,1) ) - k_x₁ = ((0 * 2) + (0 * 0) + (0 * 5) + (-M * 0) + (-M * 0) ) - 3 = -3;

Max_x₂ = ((Cb₁ * x_1,2) + (Cb₂ * x_2,2) + (Cb₃ * x_3,2) + (Cb₄ * x_4,2) + (Cb₅ * x_5,2) ) - k_x₂ = ((0 * 1) + (0 * 0) + (0 * 4) + (-M * 2) + (-M * 0) ) - 4 = -2M-4;

Max_x₃ = ((Cb₁ * x_1,3) + (Cb₂ * x_2,3) + (Cb₃ * x_3,3) + (Cb₄ * x_4,3) + (Cb₅ * x_5,3) ) - k_x₃ = ((0 * 1) + (0 * 0) + (0 * 0) + (-M * 0) + (-M * 0) ) - 0 = 0;

Max_x₄ = ((Cb₁ * x_1,4) + (Cb₂ * x_2,4) + (Cb₃ * x_3,4) + (Cb₄ * x_4,4) + (Cb₅ * x_5,4) ) - k_x₄ = ((0 * 0) + (0 * 1) + (0 * 0) + (-M * 0) + (-M * 0) ) - 0 = 0;

Max_x₅ = ((Cb₁ * x_1,5) + (Cb₂ * x_2,5) + (Cb₃ * x_3,5) + (Cb₄ * x_4,5) + (Cb₅ * x_5,5) ) - k_x₅ = ((0 * 0) + (0 * 0) + (0 * 1) + (-M * 0) + (-M * 0) ) - 0 = 0;

Max_x₆ = ((Cb₁ * x_1,6) + (Cb₂ * x_2,6) + (Cb₃ * x_3,6) + (Cb₄ * x_4,6) + (Cb₅ * x_5,6) ) - k_x₆ = ((0 * 0) + (0 * 0) + (0 * 0) + (-M * -1) + (-M * 0) ) - 0 = M;

Max_x₇ = ((Cb₁ * x_1,7) + (Cb₂ * x_2,7) + (Cb₃ * x_3,7) + (Cb₄ * x_4,7) + (Cb₅ * x_5,7) ) - k_x₇ = ((0 * 0) + (0 * 0) + (0 * 0) + (-M * 0) + (-M * -1) ) - 0 = M;

Max_x₈ = ((Cb₁ * x_1,8) + (Cb₂ * x_2,8) + (Cb₃ * x_3,8) + (Cb₄ * x_4,8) + (Cb₅ * x_5,8) ) - k_x₈ = ((0 * 0) + (0 * 0) + (0 * 0) + (-M * 1) + (-M * 0) ) - -M = 0;

Max_x₉ = ((Cb₁ * x_1,9) + (Cb₂ * x_2,9) + (Cb₃ * x_3,9) + (Cb₄ * x_4,9) + (Cb₅ * x_5,9) ) - k_x₉ = ((0 * 0) + (0 * 0) + (0 * 0) + (-M * 0) + (-M * 1) ) - -M = 0;

Q column items

Since there are negative values among the estimates of the controlled variables, the current table does not yet have an optimal solution. Therefore, in the basis we introduce the variable with the smallest negative estimate.

The number of variables in the basis is always constant, so it is necessary to choose which variable to derive from the basis, for which we calculate Q.

The elements of the Q column are calculated by dividing the values from column P by the value from the column corresponding to the variable that is entered in the basis:

Q₁ = P₁ / x_1,2 = 600 / 1 = 600;

Q₂ = P₂ / x_2,2 = 225 / 0 = ∞;

Q₃ = P₃ / x_3,2 = 1000 / 4 = 250;

Q₄ = P₄ / x_4,2 = 150 / 2 = 75;

Q₅ = P₅ / x_5,2 = 0 / 0 = ∞;

We deduce from the basis the variable with the least positive value of Q.

At the intersection of the line that corresponds to the variable that is derived from the basis, and the column that corresponds to the variable that is entered into the basis, is the resolving element.

This element will allow us to calculate the elements of the table of the next iteration.

Iteration: 2

B	Cb	P	x₁↓	x₂	x₃	x₄	x₅	x₆	x₇	x₈	x₉	Q
B	Cb	P	3	4	0	0	0	0	0	-M	-M	Q
x₃	0	525	2	0	1	0	0	0.5	0	-0.5	0	262.5
x₄	0	225	0	0	0	1	0	0	0	0	0	∞
x₅ ←	0	700	5	0	0	0	1	2	0	-2	0	140
x₂	4	75	0	1	0	0	0	-0.5	0	0.5	0	∞
x₉	-M	0	0	0	0	0	0	0	-1	0	1	∞
max		300	-3	0	0	0	0	-2	M	M+2	0

Calculation of table elements: arrow down description

Elements of the column basis (B)

For the results of the calculations of the previous iteration, we remove the variable from the basis x₈ and put in her place x₂. All other cells remain unchanged.

Cb column items

Each cell of this column is equal to the coefficient, which corresponds to the base variable in the corresponding row.

Cb₁ = 0;

Cb₂ = 0;

Cb₃ = 0;

Cb₄ = 4;

Cb₅ = -M;

Values of variable variables and column P(The data from the previous iteration is taken as the initial data)

Fill all cells with zeros corresponding to the variable that has just been entered into the basis:(The resolution element remains unchanged)

x_1,2 = 0;

x_2,2 = 0;

x_3,2 = 0;

x_5,2 = 0;

We transfer the row with the resolving element from the previous table into the current table, elementwise dividing its values into the resolving element:

P₄ = P₄ / x_4,2 = 150 / 2 = 75;

x_4,1 = x_4,1 / x_4,2 = 0 / 2 = 0;

x_4,2 = x_4,2 / x_4,2 = 2 / 2 = 1;

x_4,3 = x_4,3 / x_4,2 = 0 / 2 = 0;

x_4,4 = x_4,4 / x_4,2 = 0 / 2 = 0;

x_4,5 = x_4,5 / x_4,2 = 0 / 2 = 0;

x_4,6 = x_4,6 / x_4,2 = -1 / 2 = -0.5;

x_4,7 = x_4,7 / x_4,2 = 0 / 2 = 0;

x_4,8 = x_4,8 / x_4,2 = 1 / 2 = 0.5;

x_4,9 = x_4,9 / x_4,2 = 0 / 2 = 0;

The remaining empty cells, except for the row of estimates and the column Q, are calculated using the rectangle method, relative to the resolving element:

P₁ = (P₁ * x_4,2) - (x_1,2 * P₄) / x_4,2 = ((600 * 2) - (1 * 150)) / 2 = 525;

P₂ = (P₂ * x_4,2) - (x_2,2 * P₄) / x_4,2 = ((225 * 2) - (0 * 150)) / 2 = 225;

P₃ = (P₃ * x_4,2) - (x_3,2 * P₄) / x_4,2 = ((1000 * 2) - (4 * 150)) / 2 = 700;

P₅ = (P₅ * x_4,2) - (x_5,2 * P₄) / x_4,2 = ((0 * 2) - (0 * 150)) / 2 = 0;

x_1,1 = ((x_1,1 * x_4,2) - (x_1,2 * x_4,1)) / x_4,2 = ((2 * 2) - (1 * 0)) / 2 = 2;

x_1,2 = ((x_1,2 * x_4,2) - (x_1,2 * x_4,2)) / x_4,2 = ((1 * 2) - (1 * 2)) / 2 = 0;

x_1,4 = ((x_1,4 * x_4,2) - (x_1,2 * x_4,4)) / x_4,2 = ((0 * 2) - (1 * 0)) / 2 = 0;

x_1,5 = ((x_1,5 * x_4,2) - (x_1,2 * x_4,5)) / x_4,2 = ((0 * 2) - (1 * 0)) / 2 = 0;

x_1,6 = ((x_1,6 * x_4,2) - (x_1,2 * x_4,6)) / x_4,2 = ((0 * 2) - (1 * -1)) / 2 = 0.5;

x_1,7 = ((x_1,7 * x_4,2) - (x_1,2 * x_4,7)) / x_4,2 = ((0 * 2) - (1 * 0)) / 2 = 0;

x_1,8 = ((x_1,8 * x_4,2) - (x_1,2 * x_4,8)) / x_4,2 = ((0 * 2) - (1 * 1)) / 2 = -0.5;

x_1,9 = ((x_1,9 * x_4,2) - (x_1,2 * x_4,9)) / x_4,2 = ((0 * 2) - (1 * 0)) / 2 = 0;

x_2,1 = ((x_2,1 * x_4,2) - (x_2,2 * x_4,1)) / x_4,2 = ((0 * 2) - (0 * 0)) / 2 = 0;

x_2,2 = ((x_2,2 * x_4,2) - (x_2,2 * x_4,2)) / x_4,2 = ((0 * 2) - (0 * 2)) / 2 = 0;

x_2,4 = ((x_2,4 * x_4,2) - (x_2,2 * x_4,4)) / x_4,2 = ((1 * 2) - (0 * 0)) / 2 = 1;

x_2,5 = ((x_2,5 * x_4,2) - (x_2,2 * x_4,5)) / x_4,2 = ((0 * 2) - (0 * 0)) / 2 = 0;

x_2,6 = ((x_2,6 * x_4,2) - (x_2,2 * x_4,6)) / x_4,2 = ((0 * 2) - (0 * -1)) / 2 = 0;

x_2,7 = ((x_2,7 * x_4,2) - (x_2,2 * x_4,7)) / x_4,2 = ((0 * 2) - (0 * 0)) / 2 = 0;

x_2,8 = ((x_2,8 * x_4,2) - (x_2,2 * x_4,8)) / x_4,2 = ((0 * 2) - (0 * 1)) / 2 = 0;

x_2,9 = ((x_2,9 * x_4,2) - (x_2,2 * x_4,9)) / x_4,2 = ((0 * 2) - (0 * 0)) / 2 = 0;

x_3,1 = ((x_3,1 * x_4,2) - (x_3,2 * x_4,1)) / x_4,2 = ((5 * 2) - (4 * 0)) / 2 = 5;

x_3,2 = ((x_3,2 * x_4,2) - (x_3,2 * x_4,2)) / x_4,2 = ((4 * 2) - (4 * 2)) / 2 = 0;

x_3,4 = ((x_3,4 * x_4,2) - (x_3,2 * x_4,4)) / x_4,2 = ((0 * 2) - (4 * 0)) / 2 = 0;

x_3,5 = ((x_3,5 * x_4,2) - (x_3,2 * x_4,5)) / x_4,2 = ((1 * 2) - (4 * 0)) / 2 = 1;

x_3,6 = ((x_3,6 * x_4,2) - (x_3,2 * x_4,6)) / x_4,2 = ((0 * 2) - (4 * -1)) / 2 = 2;

x_3,7 = ((x_3,7 * x_4,2) - (x_3,2 * x_4,7)) / x_4,2 = ((0 * 2) - (4 * 0)) / 2 = 0;

x_3,8 = ((x_3,8 * x_4,2) - (x_3,2 * x_4,8)) / x_4,2 = ((0 * 2) - (4 * 1)) / 2 = -2;

x_3,9 = ((x_3,9 * x_4,2) - (x_3,2 * x_4,9)) / x_4,2 = ((0 * 2) - (4 * 0)) / 2 = 0;

x_5,1 = ((x_5,1 * x_4,2) - (x_5,2 * x_4,1)) / x_4,2 = ((0 * 2) - (0 * 0)) / 2 = 0;

x_5,2 = ((x_5,2 * x_4,2) - (x_5,2 * x_4,2)) / x_4,2 = ((0 * 2) - (0 * 2)) / 2 = 0;

x_5,4 = ((x_5,4 * x_4,2) - (x_5,2 * x_4,4)) / x_4,2 = ((0 * 2) - (0 * 0)) / 2 = 0;

x_5,5 = ((x_5,5 * x_4,2) - (x_5,2 * x_4,5)) / x_4,2 = ((0 * 2) - (0 * 0)) / 2 = 0;

x_5,6 = ((x_5,6 * x_4,2) - (x_5,2 * x_4,6)) / x_4,2 = ((0 * 2) - (0 * -1)) / 2 = 0;

x_5,7 = ((x_5,7 * x_4,2) - (x_5,2 * x_4,7)) / x_4,2 = ((-1 * 2) - (0 * 0)) / 2 = -1;

x_5,8 = ((x_5,8 * x_4,2) - (x_5,2 * x_4,8)) / x_4,2 = ((0 * 2) - (0 * 1)) / 2 = 0;

x_5,9 = ((x_5,9 * x_4,2) - (x_5,2 * x_4,9)) / x_4,2 = ((1 * 2) - (0 * 0)) / 2 = 1;

Objective function value

We calculate the value of the objective function by elementwise multiplying the column Cb by the column P, adding the results of the products.

Max_P = (Cb₁ * P₁) + (Cb₁₁ * P₂ + (Cb₂₁ * P₃ + (Cb₃₁ * P₄ + (Cb₄₁ * P₅ = (0 * 525) + (0 * 225) + (0 * 700) + (4 * 75) + (-M * 0) = 300;

Evaluated Control Variables

Max_x₁ = ((Cb₁ * x_1,1) + (Cb₂ * x_2,1) + (Cb₃ * x_3,1) + (Cb₄ * x_4,1) + (Cb₅ * x_5,1) ) - k_x₁ = ((0 * 2) + (0 * 0) + (0 * 5) + (4 * 0) + (-M * 0) ) - 3 = -3;

Max_x₂ = ((Cb₁ * x_1,2) + (Cb₂ * x_2,2) + (Cb₃ * x_3,2) + (Cb₄ * x_4,2) + (Cb₅ * x_5,2) ) - k_x₂ = ((0 * 0) + (0 * 0) + (0 * 0) + (4 * 1) + (-M * 0) ) - 4 = 0;

Max_x₃ = ((Cb₁ * x_1,3) + (Cb₂ * x_2,3) + (Cb₃ * x_3,3) + (Cb₄ * x_4,3) + (Cb₅ * x_5,3) ) - k_x₃ = ((0 * 1) + (0 * 0) + (0 * 0) + (4 * 0) + (-M * 0) ) - 0 = 0;

Max_x₄ = ((Cb₁ * x_1,4) + (Cb₂ * x_2,4) + (Cb₃ * x_3,4) + (Cb₄ * x_4,4) + (Cb₅ * x_5,4) ) - k_x₄ = ((0 * 0) + (0 * 1) + (0 * 0) + (4 * 0) + (-M * 0) ) - 0 = 0;

Max_x₅ = ((Cb₁ * x_1,5) + (Cb₂ * x_2,5) + (Cb₃ * x_3,5) + (Cb₄ * x_4,5) + (Cb₅ * x_5,5) ) - k_x₅ = ((0 * 0) + (0 * 0) + (0 * 1) + (4 * 0) + (-M * 0) ) - 0 = 0;

Max_x₆ = ((Cb₁ * x_1,6) + (Cb₂ * x_2,6) + (Cb₃ * x_3,6) + (Cb₄ * x_4,6) + (Cb₅ * x_5,6) ) - k_x₆ = ((0 * 0.5) + (0 * 0) + (0 * 2) + (4 * -0.5) + (-M * 0) ) - 0 = -2;

Max_x₇ = ((Cb₁ * x_1,7) + (Cb₂ * x_2,7) + (Cb₃ * x_3,7) + (Cb₄ * x_4,7) + (Cb₅ * x_5,7) ) - k_x₇ = ((0 * 0) + (0 * 0) + (0 * 0) + (4 * 0) + (-M * -1) ) - 0 = M;

Max_x₈ = ((Cb₁ * x_1,8) + (Cb₂ * x_2,8) + (Cb₃ * x_3,8) + (Cb₄ * x_4,8) + (Cb₅ * x_5,8) ) - k_x₈ = ((0 * -0.5) + (0 * 0) + (0 * -2) + (4 * 0.5) + (-M * 0) ) - -M = M+2;

Max_x₉ = ((Cb₁ * x_1,9) + (Cb₂ * x_2,9) + (Cb₃ * x_3,9) + (Cb₄ * x_4,9) + (Cb₅ * x_5,9) ) - k_x₉ = ((0 * 0) + (0 * 0) + (0 * 0) + (4 * 0) + (-M * 1) ) - -M = 0;

Q column items

The number of variables in the basis is always constant, so it is necessary to choose which variable to derive from the basis, for which we calculate Q.

The elements of the Q column are calculated by dividing the values from column P by the value from the column corresponding to the variable that is entered in the basis:

Q₁ = P₁ / x_1,1 = 525 / 2 = 262.5;

Q₂ = P₂ / x_2,1 = 225 / 0 = ∞;

Q₃ = P₃ / x_3,1 = 700 / 5 = 140;

Q₄ = P₄ / x_4,1 = 75 / 0 = ∞;

Q₅ = P₅ / x_5,1 = 0 / 0 = ∞;

We deduce from the basis the variable with the least positive value of Q.

This element will allow us to calculate the elements of the table of the next iteration.

Iteration: 3

B	Cb	P	x₁	x₂	x₃	x₄	x₅	x₆↓	x₇	x₈	x₉	Q
B	Cb	P	3	4	0	0	0	0	0	-M	-M	Q
x₃	0	245	0	0	1	0	-0.4	-0.3	0	0.3	0	-816.67
x₄	0	225	0	0	0	1	0	0	0	0	0	∞
x₁ ←	3	140	1	0	0	0	0.2	0.4	0	-0.4	0	350
x₂	4	75	0	1	0	0	0	-0.5	0	0.5	0	-150
x₉	-M	0	0	0	0	0	0	0	-1	0	1	∞
max		720	0	0	0	0	0.6	-0.8	M	M+0.8	0

Calculation of table elements: arrow down description

Elements of the column basis (B)

For the results of the calculations of the previous iteration, we remove the variable from the basis x₅ and put in her place x₁. All other cells remain unchanged.

Cb column items

Each cell of this column is equal to the coefficient, which corresponds to the base variable in the corresponding row.

Cb₁ = 0;

Cb₂ = 0;

Cb₃ = 3;

Cb₄ = 4;

Cb₅ = -M;

Values of variable variables and column P(The data from the previous iteration is taken as the initial data)

Fill all cells with zeros corresponding to the variable that has just been entered into the basis:(The resolution element remains unchanged)

x_1,1 = 0;

x_2,1 = 0;

x_4,1 = 0;

x_5,1 = 0;

We transfer the row with the resolving element from the previous table into the current table, elementwise dividing its values into the resolving element:

P₃ = P₃ / x_3,1 = 700 / 5 = 140;

x_3,1 = x_3,1 / x_3,1 = 5 / 5 = 1;

x_3,2 = x_3,2 / x_3,1 = 0 / 5 = 0;

x_3,3 = x_3,3 / x_3,1 = 0 / 5 = 0;

x_3,4 = x_3,4 / x_3,1 = 0 / 5 = 0;

x_3,5 = x_3,5 / x_3,1 = 1 / 5 = 0.2;

x_3,6 = x_3,6 / x_3,1 = 2 / 5 = 0.4;

x_3,7 = x_3,7 / x_3,1 = 0 / 5 = 0;

x_3,8 = x_3,8 / x_3,1 = -2 / 5 = -0.4;

x_3,9 = x_3,9 / x_3,1 = 0 / 5 = 0;

The remaining empty cells, except for the row of estimates and the column Q, are calculated using the rectangle method, relative to the resolving element:

P₁ = (P₁ * x_3,1) - (x_1,1 * P₃) / x_3,1 = ((525 * 5) - (2 * 700)) / 5 = 245;

P₂ = (P₂ * x_3,1) - (x_2,1 * P₃) / x_3,1 = ((225 * 5) - (0 * 700)) / 5 = 225;

P₄ = (P₄ * x_3,1) - (x_4,1 * P₃) / x_3,1 = ((75 * 5) - (0 * 700)) / 5 = 75;

P₅ = (P₅ * x_3,1) - (x_5,1 * P₃) / x_3,1 = ((0 * 5) - (0 * 700)) / 5 = 0;

x_1,1 = ((x_1,1 * x_3,1) - (x_1,1 * x_3,1)) / x_3,1 = ((2 * 5) - (2 * 5)) / 5 = 0;

x_1,3 = ((x_1,3 * x_3,1) - (x_1,1 * x_3,3)) / x_3,1 = ((1 * 5) - (2 * 0)) / 5 = 1;

x_1,4 = ((x_1,4 * x_3,1) - (x_1,1 * x_3,4)) / x_3,1 = ((0 * 5) - (2 * 0)) / 5 = 0;

x_1,5 = ((x_1,5 * x_3,1) - (x_1,1 * x_3,5)) / x_3,1 = ((0 * 5) - (2 * 1)) / 5 = -0.4;

x_1,6 = ((x_1,6 * x_3,1) - (x_1,1 * x_3,6)) / x_3,1 = ((0.5 * 5) - (2 * 2)) / 5 = -0.3;

x_1,7 = ((x_1,7 * x_3,1) - (x_1,1 * x_3,7)) / x_3,1 = ((0 * 5) - (2 * 0)) / 5 = 0;

x_1,8 = ((x_1,8 * x_3,1) - (x_1,1 * x_3,8)) / x_3,1 = ((-0.5 * 5) - (2 * -2)) / 5 = 0.3;

x_1,9 = ((x_1,9 * x_3,1) - (x_1,1 * x_3,9)) / x_3,1 = ((0 * 5) - (2 * 0)) / 5 = 0;

x_2,1 = ((x_2,1 * x_3,1) - (x_2,1 * x_3,1)) / x_3,1 = ((0 * 5) - (0 * 5)) / 5 = 0;

x_2,3 = ((x_2,3 * x_3,1) - (x_2,1 * x_3,3)) / x_3,1 = ((0 * 5) - (0 * 0)) / 5 = 0;

x_2,4 = ((x_2,4 * x_3,1) - (x_2,1 * x_3,4)) / x_3,1 = ((1 * 5) - (0 * 0)) / 5 = 1;

x_2,5 = ((x_2,5 * x_3,1) - (x_2,1 * x_3,5)) / x_3,1 = ((0 * 5) - (0 * 1)) / 5 = 0;

x_2,6 = ((x_2,6 * x_3,1) - (x_2,1 * x_3,6)) / x_3,1 = ((0 * 5) - (0 * 2)) / 5 = 0;

x_2,7 = ((x_2,7 * x_3,1) - (x_2,1 * x_3,7)) / x_3,1 = ((0 * 5) - (0 * 0)) / 5 = 0;

x_2,8 = ((x_2,8 * x_3,1) - (x_2,1 * x_3,8)) / x_3,1 = ((0 * 5) - (0 * -2)) / 5 = 0;

x_2,9 = ((x_2,9 * x_3,1) - (x_2,1 * x_3,9)) / x_3,1 = ((0 * 5) - (0 * 0)) / 5 = 0;

x_4,1 = ((x_4,1 * x_3,1) - (x_4,1 * x_3,1)) / x_3,1 = ((0 * 5) - (0 * 5)) / 5 = 0;

x_4,3 = ((x_4,3 * x_3,1) - (x_4,1 * x_3,3)) / x_3,1 = ((0 * 5) - (0 * 0)) / 5 = 0;

x_4,4 = ((x_4,4 * x_3,1) - (x_4,1 * x_3,4)) / x_3,1 = ((0 * 5) - (0 * 0)) / 5 = 0;

x_4,5 = ((x_4,5 * x_3,1) - (x_4,1 * x_3,5)) / x_3,1 = ((0 * 5) - (0 * 1)) / 5 = 0;

x_4,6 = ((x_4,6 * x_3,1) - (x_4,1 * x_3,6)) / x_3,1 = ((-0.5 * 5) - (0 * 2)) / 5 = -0.5;

x_4,7 = ((x_4,7 * x_3,1) - (x_4,1 * x_3,7)) / x_3,1 = ((0 * 5) - (0 * 0)) / 5 = 0;

x_4,8 = ((x_4,8 * x_3,1) - (x_4,1 * x_3,8)) / x_3,1 = ((0.5 * 5) - (0 * -2)) / 5 = 0.5;

x_4,9 = ((x_4,9 * x_3,1) - (x_4,1 * x_3,9)) / x_3,1 = ((0 * 5) - (0 * 0)) / 5 = 0;

x_5,1 = ((x_5,1 * x_3,1) - (x_5,1 * x_3,1)) / x_3,1 = ((0 * 5) - (0 * 5)) / 5 = 0;

x_5,3 = ((x_5,3 * x_3,1) - (x_5,1 * x_3,3)) / x_3,1 = ((0 * 5) - (0 * 0)) / 5 = 0;

x_5,4 = ((x_5,4 * x_3,1) - (x_5,1 * x_3,4)) / x_3,1 = ((0 * 5) - (0 * 0)) / 5 = 0;

x_5,5 = ((x_5,5 * x_3,1) - (x_5,1 * x_3,5)) / x_3,1 = ((0 * 5) - (0 * 1)) / 5 = 0;

x_5,6 = ((x_5,6 * x_3,1) - (x_5,1 * x_3,6)) / x_3,1 = ((0 * 5) - (0 * 2)) / 5 = 0;

x_5,7 = ((x_5,7 * x_3,1) - (x_5,1 * x_3,7)) / x_3,1 = ((-1 * 5) - (0 * 0)) / 5 = -1;

x_5,8 = ((x_5,8 * x_3,1) - (x_5,1 * x_3,8)) / x_3,1 = ((0 * 5) - (0 * -2)) / 5 = 0;

x_5,9 = ((x_5,9 * x_3,1) - (x_5,1 * x_3,9)) / x_3,1 = ((1 * 5) - (0 * 0)) / 5 = 1;

Objective function value

We calculate the value of the objective function by elementwise multiplying the column Cb by the column P, adding the results of the products.

Max_P = (Cb₁ * P₁) + (Cb₁₁ * P₂ + (Cb₂₁ * P₃ + (Cb₃₁ * P₄ + (Cb₄₁ * P5) = (0 * 245) + (0 * 225) + (3 * 140) + (4 * 75) + (-M * 0) = 720;

Evaluated Control Variables

Max_x₁ = ((Cb₁ * x_1,1) + (Cb₂ * x_2,1) + (Cb₃ * x_3,1) + (Cb₄ * x_4,1) + (Cb₅ * x_5,1) ) - k_x₁ = ((0 * 0) + (0 * 0) + (3 * 1) + (4 * 0) + (-M * 0) ) - 3 = 0;

Max_x₂ = ((Cb₁ * x_1,2) + (Cb₂ * x_2,2) + (Cb₃ * x_3,2) + (Cb₄ * x_4,2) + (Cb₅ * x_5,2) ) - k_x₂ = ((0 * 0) + (0 * 0) + (3 * 0) + (4 * 1) + (-M * 0) ) - 4 = 0;

Max_x₃ = ((Cb₁ * x_1,3) + (Cb₂ * x_2,3) + (Cb₃ * x_3,3) + (Cb₄ * x_4,3) + (Cb₅ * x_5,3) ) - k_x₃ = ((0 * 1) + (0 * 0) + (3 * 0) + (4 * 0) + (-M * 0) ) - 0 = 0;

Max_x₄ = ((Cb₁ * x_1,4) + (Cb₂ * x_2,4) + (Cb₃ * x_3,4) + (Cb₄ * x_4,4) + (Cb₅ * x_5,4) ) - k_x₄ = ((0 * 0) + (0 * 1) + (3 * 0) + (4 * 0) + (-M * 0) ) - 0 = 0;

Max_x₅ = ((Cb₁ * x_1,5) + (Cb₂ * x_2,5) + (Cb₃ * x_3,5) + (Cb₄ * x_4,5) + (Cb₅ * x_5,5) ) - k_x₅ = ((0 * -0.4) + (0 * 0) + (3 * 0.2) + (4 * 0) + (-M * 0) ) - 0 = 0.6;

Max_x₆ = ((Cb₁ * x_1,6) + (Cb₂ * x_2,6) + (Cb₃ * x_3,6) + (Cb₄ * x_4,6) + (Cb₅ * x_5,6) ) - k_x₆ = ((0 * -0.3) + (0 * 0) + (3 * 0.4) + (4 * -0.5) + (-M * 0) ) - 0 = -0.8;

Max_x₇ = ((Cb₁ * x_1,7) + (Cb₂ * x_2,7) + (Cb₃ * x_3,7) + (Cb₄ * x_4,7) + (Cb₅ * x_5,7) ) - k_x₇ = ((0 * 0) + (0 * 0) + (3 * 0) + (4 * 0) + (-M * -1) ) - 0 = M;

Max_x₈ = ((Cb₁ * x_1,8) + (Cb₂ * x_2,8) + (Cb₃ * x_3,8) + (Cb₄ * x_4,8) + (Cb₅ * x_5,8) ) - k_x₈ = ((0 * 0.3) + (0 * 0) + (3 * -0.4) + (4 * 0.5) + (-M * 0) ) - -M = M+0.8;

Max_x₉ = ((Cb₁ * x_1,9) + (Cb₂ * x_2,9) + (Cb₃ * x_3,9) + (Cb₄ * x_4,9) + (Cb₅ * x_5,9) ) - k_x₉ = ((0 * 0) + (0 * 0) + (3 * 0) + (4 * 0) + (-M * 1) ) - -M = 0;

Q column items

The number of variables in the basis is always constant, so it is necessary to choose which variable to derive from the basis, for which we calculate Q.

The elements of the Q column are calculated by dividing the values from column P by the value from the column corresponding to the variable that is entered in the basis:

Q₁ = P₁ / x_1,6 = 245 / -0.3 = -816.67;

Q₂ = P₂ / x_2,6 = 225 / 0 = ∞;

Q₃ = P₃ / x_3,6 = 140 / 0.4 = 350;

Q₄ = P₄ / x_4,6 = 75 / -0.5 = -150;

Q₅ = P₅ / x_5,6 = 0 / 0 = ∞;

We deduce from the basis the variable with the least positive value of Q.

This element will allow us to calculate the elements of the table of the next iteration.

Iteration: 4

B	Cb	P	x₁	x₂	x₃	x₄	x₅	x₆	x₇	x₈	x₉	Q
B	Cb	P	3	4	0	0	0	0	0	-M	-M	Q
x₃	0	350	0.75	0	1	0	-0.25	0	0	0	0
x₄	0	225	0	0	0	1	0	0	0	0	0
x₆	0	350	2.5	0	0	0	0.5	1	0	-1	0
x₂	4	250	1.25	1	0	0	0.25	0	0	0	0
x₉	-M	0	0	0	0	0	0	0	-1	0	1
max		1000	2	0	0	0	1	0	M	M	0

Calculation of table elements: arrow down description

Elements of the column basis (B)

For the results of the calculations of the previous iteration, we remove the variable from the basis x₁ and put in her place x₆. All other cells remain unchanged.

Cb column items

Each cell of this column is equal to the coefficient, which corresponds to the base variable in the corresponding row.

Cb₁ = 0;

Cb₂ = 0;

Cb₃ = 0;

Cb₄ = 4;

Cb₅ = -M;

Values of variable variables and column P(The data from the previous iteration is taken as the initial data)

Fill all cells with zeros corresponding to the variable that has just been entered into the basis:(The resolution element remains unchanged)

x_1,6 = 0;

x_2,6 = 0;

x_4,6 = 0;

x_5,6 = 0;

We transfer the row with the resolving element from the previous table into the current table, elementwise dividing its values into the resolving element:

P₃ = P₃ / x_3,6 = 140 / 0.4 = 350;

x_3,1 = x_3,1 / x_3,6 = 1 / 0.4 = 2.5;

x_3,2 = x_3,2 / x_3,6 = 0 / 0.4 = 0;

x_3,3 = x_3,3 / x_3,6 = 0 / 0.4 = 0;

x_3,4 = x_3,4 / x_3,6 = 0 / 0.4 = 0;

x_3,5 = x_3,5 / x_3,6 = 0.2 / 0.4 = 0.5;

x_3,6 = x_3,6 / x_3,6 = 0.4 / 0.4 = 1;

x_3,7 = x_3,7 / x_3,6 = 0 / 0.4 = 0;

x_3,8 = x_3,8 / x_3,6 = -0.4 / 0.4 = -1;

x_3,9 = x_3,9 / x_3,6 = 0 / 0.4 = 0;

The remaining empty cells, except for the row of estimates and the column Q, are calculated using the rectangle method, relative to the resolving element:

P₁ = (P₁ * x_3,6) - (x_1,6 * P₃) / x_3,6 = ((245 * 0.4) - (-0.3 * 140)) / 0.4 = 350;

P₂ = (P₂ * x_3,6) - (x_2,6 * P₃) / x_3,6 = ((225 * 0.4) - (0 * 140)) / 0.4 = 225;

P₄ = (P₄ * x_3,6) - (x_4,6 * P₃) / x_3,6 = ((75 * 0.4) - (-0.5 * 140)) / 0.4 = 250;

P₅ = (P₅ * x_3,6) - (x_5,6 * P₃) / x_3,6 = ((0 * 0.4) - (0 * 140)) / 0.4 = 0;

x_1,1 = ((x_1,1 * x_3,6) - (x_1,6 * x_3,1)) / x_3,6 = ((0 * 0.4) - (-0.3 * 1)) / 0.4 = 0.75;

x_1,2 = ((x_1,2 * x_3,6) - (x_1,6 * x_3,2)) / x_3,6 = ((0 * 0.4) - (-0.3 * 0)) / 0.4 = 0;

x_1,3 = ((x_1,3 * x_3,6) - (x_1,6 * x_3,3)) / x_3,6 = ((1 * 0.4) - (-0.3 * 0)) / 0.4 = 1;

x_1,4 = ((x_1,4 * x_3,6) - (x_1,6 * x_3,4)) / x_3,6 = ((0 * 0.4) - (-0.3 * 0)) / 0.4 = 0;

x_1,5 = ((x_1,5 * x_3,6) - (x_1,6 * x_3,5)) / x_3,6 = ((-0.4 * 0.4) - (-0.3 * 0.2)) / 0.4 = -0.25;

x_1,6 = ((x_1,6 * x_3,6) - (x_1,6 * x_3,6)) / x_3,6 = ((-0.3 * 0.4) - (-0.3 * 0.4)) / 0.4 = 0;

x_1,8 = ((x_1,8 * x_3,6) - (x_1,6 * x_3,8)) / x_3,6 = ((0.3 * 0.4) - (-0.3 * -0.4)) / 0.4 = 0;

x_1,9 = ((x_1,9 * x_3,6) - (x_1,6 * x_3,9)) / x_3,6 = ((0 * 0.4) - (-0.3 * 0)) / 0.4 = 0;

x_2,1 = ((x_2,1 * x_3,6) - (x_2,6 * x_3,1)) / x_3,6 = ((0 * 0.4) - (0 * 1)) / 0.4 = 0;

x_2,2 = ((x_2,2 * x_3,6) - (x_2,6 * x_3,2)) / x_3,6 = ((0 * 0.4) - (0 * 0)) / 0.4 = 0;

x_2,3 = ((x_2,3 * x_3,6) - (x_2,6 * x_3,3)) / x_3,6 = ((0 * 0.4) - (0 * 0)) / 0.4 = 0;

x_2,4 = ((x_2,4 * x_3,6) - (x_2,6 * x_3,4)) / x_3,6 = ((1 * 0.4) - (0 * 0)) / 0.4 = 1;

x_2,5 = ((x_2,5 * x_3,6) - (x_2,6 * x_3,5)) / x_3,6 = ((0 * 0.4) - (0 * 0.2)) / 0.4 = 0;

x_2,6 = ((x_2,6 * x_3,6) - (x_2,6 * x_3,6)) / x_3,6 = ((0 * 0.4) - (0 * 0.4)) / 0.4 = 0;

x_2,8 = ((x_2,8 * x_3,6) - (x_2,6 * x_3,8)) / x_3,6 = ((0 * 0.4) - (0 * -0.4)) / 0.4 = 0;

x_2,9 = ((x_2,9 * x_3,6) - (x_2,6 * x_3,9)) / x_3,6 = ((0 * 0.4) - (0 * 0)) / 0.4 = 0;

x_4,1 = ((x_4,1 * x_3,6) - (x_4,6 * x_3,1)) / x_3,6 = ((0 * 0.4) - (-0.5 * 1)) / 0.4 = 1.25;

x_4,2 = ((x_4,2 * x_3,6) - (x_4,6 * x_3,2)) / x_3,6 = ((1 * 0.4) - (-0.5 * 0)) / 0.4 = 1;

x_4,3 = ((x_4,3 * x_3,6) - (x_4,6 * x_3,3)) / x_3,6 = ((0 * 0.4) - (-0.5 * 0)) / 0.4 = 0;

x_4,4 = ((x_4,4 * x_3,6) - (x_4,6 * x_3,4)) / x_3,6 = ((0 * 0.4) - (-0.5 * 0)) / 0.4 = 0;

x_4,5 = ((x_4,5 * x_3,6) - (x_4,6 * x_3,5)) / x_3,6 = ((0 * 0.4) - (-0.5 * 0.2)) / 0.4 = 0.25;

x_4,6 = ((x_4,6 * x_3,6) - (x_4,6 * x_3,6)) / x_3,6 = ((-0.5 * 0.4) - (-0.5 * 0.4)) / 0.4 = 0;

x_4,8 = ((x_4,8 * x_3,6) - (x_4,6 * x_3,8)) / x_3,6 = ((0.5 * 0.4) - (-0.5 * -0.4)) / 0.4 = 0;

x_4,9 = ((x_4,9 * x_3,6) - (x_4,6 * x_3,9)) / x_3,6 = ((0 * 0.4) - (-0.5 * 0)) / 0.4 = 0;

x_5,1 = ((x_5,1 * x_3,6) - (x_5,6 * x_3,1)) / x_3,6 = ((0 * 0.4) - (0 * 1)) / 0.4 = 0;

x_5,2 = ((x_5,2 * x_3,6) - (x_5,6 * x_3,2)) / x_3,6 = ((0 * 0.4) - (0 * 0)) / 0.4 = 0;

x_5,3 = ((x_5,3 * x_3,6) - (x_5,6 * x_3,3)) / x_3,6 = ((0 * 0.4) - (0 * 0)) / 0.4 = 0;

x_5,4 = ((x_5,4 * x_3,6) - (x_5,6 * x_3,4)) / x_3,6 = ((0 * 0.4) - (0 * 0)) / 0.4 = 0;

x_5,5 = ((x_5,5 * x_3,6) - (x_5,6 * x_3,5)) / x_3,6 = ((0 * 0.4) - (0 * 0.2)) / 0.4 = 0;

x_5,6 = ((x_5,6 * x_3,6) - (x_5,6 * x_3,6)) / x_3,6 = ((0 * 0.4) - (0 * 0.4)) / 0.4 = 0;

x_5,8 = ((x_5,8 * x_3,6) - (x_5,6 * x_3,8)) / x_3,6 = ((0 * 0.4) - (0 * -0.4)) / 0.4 = 0;

x_5,9 = ((x_5,9 * x_3,6) - (x_5,6 * x_3,9)) / x_3,6 = ((1 * 0.4) - (0 * 0)) / 0.4 = 1;

Objective function value

We calculate the value of the objective function by elementwise multiplying the column Cb by the column P, adding the results of the products.

Max_P = (Cb₁ * P₁) + (Cb₁₁ * P₂ + (Cb₂₁ * P₃ + (Cb₃₁ * P₄ + (Cb₄₁ * P₅ = (0 * 350) + (0 * 225) + (0 * 350) + (4 * 250) + (-M * 0) = 1000;

Evaluated Control Variables

Max_x₁ = ((Cb₁ * x_1,1) + (Cb₂ * x_2,1) + (Cb₃ * x_3,1) + (Cb₄ * x_4,1) + (Cb₅ * x_5,1) ) - k_x₁ = ((0 * 0.75) + (0 * 0) + (0 * 2.5) + (4 * 1.25) + (-M * 0) ) - 3 = 2;

Max_x₂ = ((Cb₁ * x_1,2) + (Cb₂ * x_2,2) + (Cb₃ * x_3,2) + (Cb₄ * x_4,2) + (Cb₅ * x_5,2) ) - k_x₂ = ((0 * 0) + (0 * 0) + (0 * 0) + (4 * 1) + (-M * 0) ) - 4 = 0;

Max_x₃ = ((Cb₁ * x_1,3) + (Cb₂ * x_2,3) + (Cb₃ * x_3,3) + (Cb₄ * x_4,3) + (Cb₅ * x_5,3) ) - k_x₃ = ((0 * 1) + (0 * 0) + (0 * 0) + (4 * 0) + (-M * 0) ) - 0 = 0;

Max_x₄ = ((Cb₁ * x_1,4) + (Cb₂ * x_2,4) + (Cb₃ * x_3,4) + (Cb₄ * x_4,4) + (Cb₅ * x_5,4) ) - k_x₄ = ((0 * 0) + (0 * 1) + (0 * 0) + (4 * 0) + (-M * 0) ) - 0 = 0;

Max_x₅ = ((Cb₁ * x_1,5) + (Cb₂ * x_2,5) + (Cb₃ * x_3,5) + (Cb₄ * x_4,5) + (Cb₅ * x_5,5) ) - k_x₅ = ((0 * -0.25) + (0 * 0) + (0 * 0.5) + (4 * 0.25) + (-M * 0) ) - 0 = 1;

Max_x₆ = ((Cb₁ * x_1,6) + (Cb₂ * x_2,6) + (Cb₃ * x_3,6) + (Cb₄ * x_4,6) + (Cb₅ * x_5,6) ) - k_x₆ = ((0 * 0) + (0 * 0) + (0 * 1) + (4 * 0) + (-M * 0) ) - 0 = 0;

Max_x₇ = ((Cb₁ * x_1,7) + (Cb₂ * x_2,7) + (Cb₃ * x_3,7) + (Cb₄ * x_4,7) + (Cb₅ * x_5,7) ) - k_x₇ = ((0 * 0) + (0 * 0) + (0 * 0) + (4 * 0) + (-M * -1) ) - 0 = M;

Max_x₈ = ((Cb₁ * x_1,8) + (Cb₂ * x_2,8) + (Cb₃ * x_3,8) + (Cb₄ * x_4,8) + (Cb₅ * x_5,8) ) - k_x₈ = ((0 * 0) + (0 * 0) + (0 * -1) + (4 * 0) + (-M * 0) ) - -M = M;

Max_x₉ = ((Cb₁ * x_1,9) + (Cb₂ * x_2,9) + (Cb₃ * x_3,9) + (Cb₄ * x_4,9) + (Cb₅ * x_5,9) ) - k_x₉ = ((0 * 0) + (0 * 0) + (0 * 0) + (4 * 0) + (-M * 1) ) - -M = 0;

Result:

Since there are no negative values among the estimates of the controlled variables, the current table has an optimal solution.

The value of the objective function:

F* = 1000

The variables that are present in the basis are equal to the corresponding cells of the column P, all other variables are equal to zero:

x₁ = 0;

x₂ = 250;

Result:

F* = 1000

X* = (0; 250)

Conventions: arrow down description

x_i↓	- we enter a variable into the basis;
x_i ←	- print the variable from the base;
x_i	- permissive element;
x_i	- basic element;
B	- basis;
Cb	- coefficient at the base variable;
P	- plan;